Wie Bestimmt Man Den Scheitelpunkt
Scheitelpunktform einfach erklärt
Mit der Scheitelpunktform kannst du jede quadratische Funktion als Parabel darstellen. Sie hat die Form
f(10) = a (x – d)ii + e
Den Scheitelpunkt kannst du daran direkt ablesen, er lautet: S(d|e). a ist ein Faktor, der die Steilheit der Parabel angibt.
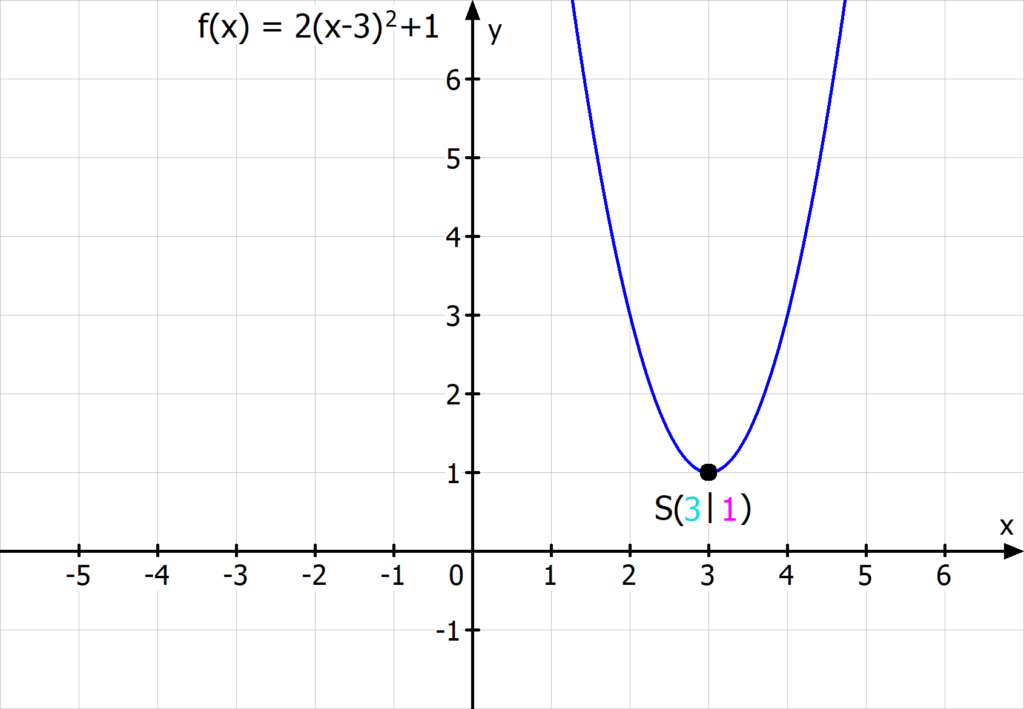
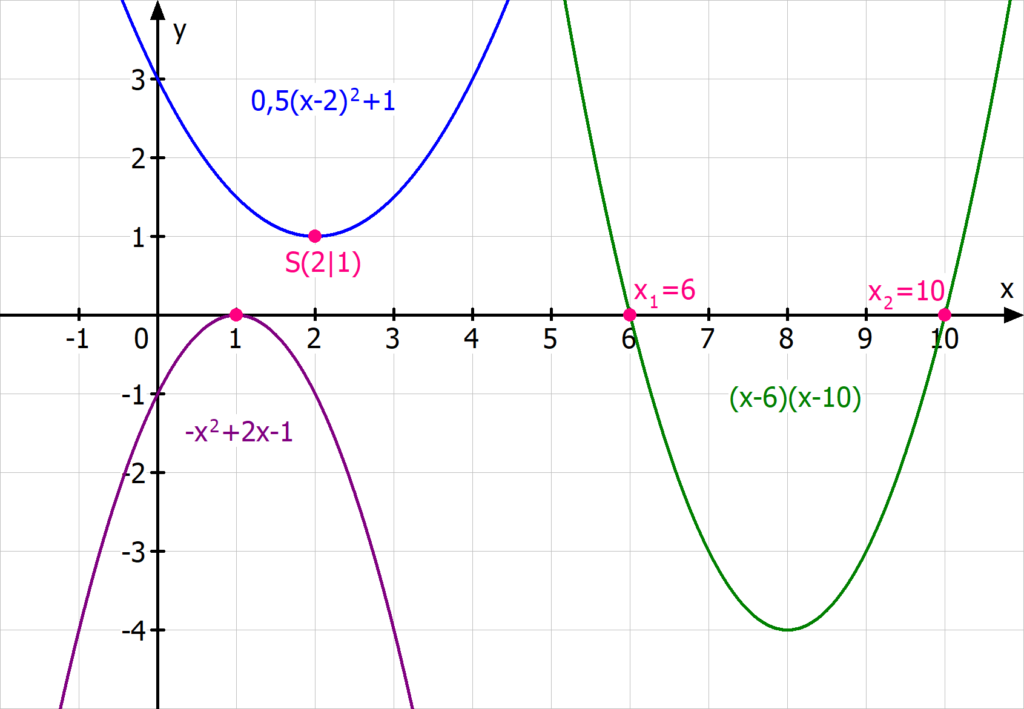
Beispiel: Der Scheitelpunkt der Funktion f(x) = 2 (x – three)ii + 1 liegt bei Due south(3|1).
Der Scheitelpunkt ist der höchster bzw. tiefster Punkt einer Parabel- abhängig davon, ob sie nach oben oder nach unten geöffnet ist.
Achtung: Pass auf, dass du kein Vorzeichen übersiehst! Wenn du beispielsweise aus f(10)=2(10 + 3)2 + 1 den Scheitelpunkt berechnen willst, erhältst du S( – 3|1)!
Scheitelpunkt berechnen
Insgesamt gibt es drei verschiedene Arten von Funktionsgleichungen , mit denen du eine quadratische Funktion beschreiben kannst. Sie lauten:
- Allgemeine Form
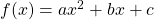 (wenn
(wenn 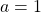 dann Normalform genannt).
dann Normalform genannt). - Faktorisierte Form
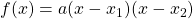 mit Nullstellen
mit Nullstellen 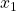 und
und 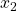 .
. - Scheitelpunktform oder Scheitelform
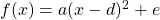 mit Scheitel
mit Scheitel 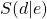 .
.
Jede dieser Formen hat Vor- und Nachteile. Welche du verwendest, hängt in erster Linie davon ab, ob du an den Nullstellen interessiert bist oder den Scheitelpunkt berechnen willst.
Wichtig ist in jedem Falle, dass der Parameter 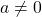 ist, da wir sonst statt einer quadratischen Funktion eine lineare Funktion erhalten würden. Das
ist, da wir sonst statt einer quadratischen Funktion eine lineare Funktion erhalten würden. Das  gibt den Öffnungsgrad der Parabel an und bestimmt, ob sie nach oben oder nach unten geöffnet ist.
gibt den Öffnungsgrad der Parabel an und bestimmt, ob sie nach oben oder nach unten geöffnet ist.
Wie du dice verschiedenen Darstellungsformen ineinander umwandelst damit du ganz einfach die Scheitelpunkte berechnen kannst, zeigen wir dir jetzt:
Allgemeine Course in Scheitelpunktform
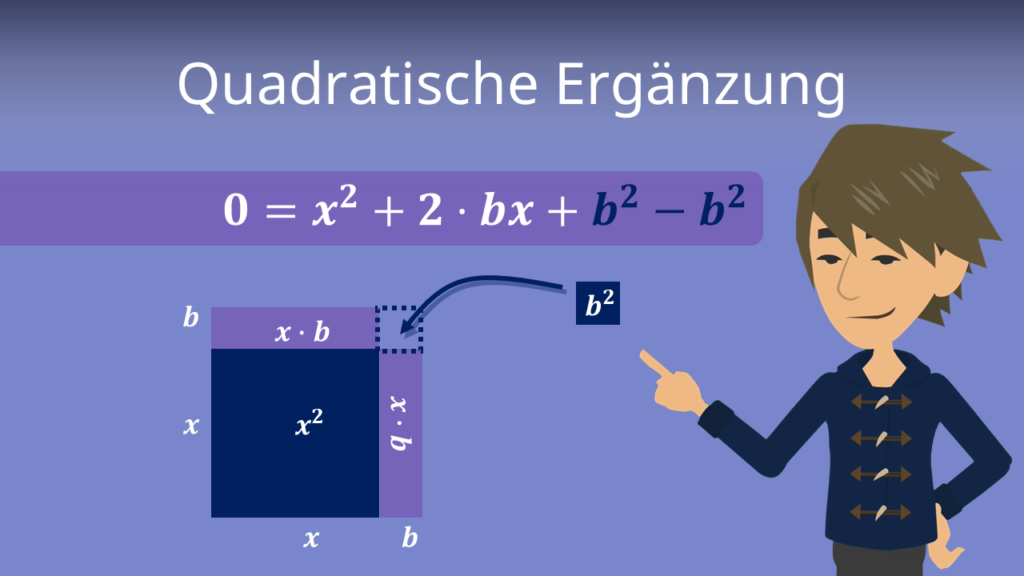
Am häufigsten rechnest du die allgemeine Grade in die Scheitelpunktform um. Die Idee dabei ist, die binomischen Formeln zu nutzen, um die beiden Formen mittels quadratischer Ergänzung ineinander umzuwandeln. Ausführlich erklären wir dies im Artikel zur quadratischen Ergänzung . Hier zeigen wir es dir konkret an einem Beispiel:
Angenommen, du willst die Scheitelform von 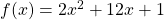 mittels quadratischer Ergänzung bestimmen.
mittels quadratischer Ergänzung bestimmen.
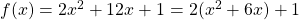
- Schritt 2: Wähle die entsprechende binomische Formel aus. Das ist hier die erste binomische Formel mit
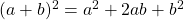
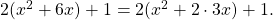
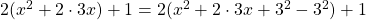
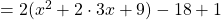
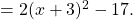
Die Scheitelpunktform von 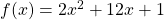 ist somit gleich
ist somit gleich 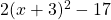 . Daraus können wir
. Daraus können wir 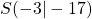 direkt ablesen und brauchen nicht extra den Scheitelpunkt berechnen.
direkt ablesen und brauchen nicht extra den Scheitelpunkt berechnen.
Analog funktioniert das Ganze natürlich auch, wenn du die Normalform in Scheitelform umrechnen möchtest.
Merke: Die Scheitelform ist ein Versuch, eine quadratische Funktion als „binomische Formel mit Rest" zu interpretieren.
Mithilfe der quadratischen Ergänzung kann man jede Parabelgleichung auf die Form einer binomischen Formel bringen:
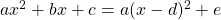
mit 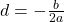 und
und 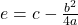 . Setzt du die Werte ein und multiplizierst die binomische Formel aus, erhältst du die linke Seite.
. Setzt du die Werte ein und multiplizierst die binomische Formel aus, erhältst du die linke Seite.
Scheitelpunktform in Allgemeine Grade
Hast du die Scheitelpunktform bereits gegeben und interessierst dich für die allgemeine Course, weil du beispielsweise mit der Mitternachtsformel die Nullstellen berechnen willst, so brauchst du keine quadratische Ergänzung. Stattdessen multiplizierst du einfach aus. Auf die gleiche Art und Weise kannst du auch die Scheitelpunktform in Normalform umrechnen.
Willst du zum Beispiel dice allgemeine Form aus der Scheitelform 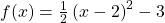 berechnen, gehst du wie folgt vor:
berechnen, gehst du wie folgt vor:
- Schritt 1: Wende dice binomische Formel an:
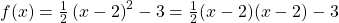
- Schritt 2: Multipliziere die Klammern aus:
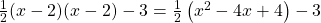
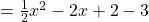
- Schritt 3: Fasse soweit wie möglich zusammen:
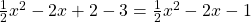
Faktorisierte Form in Scheitelpunktform
Die faktorisierte Form 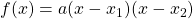 einer quadratischen Gleichung ist insbesondere bei der Nullstellenbestimmung sehr nützlich, weil du sie direkt ablesen kannst. Beispielsweise hat
einer quadratischen Gleichung ist insbesondere bei der Nullstellenbestimmung sehr nützlich, weil du sie direkt ablesen kannst. Beispielsweise hat 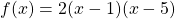 die beiden Nullstellen
die beiden Nullstellen 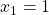 und
und 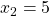 . Um diese Form möglichst geschickt in Scheitelform
. Um diese Form möglichst geschickt in Scheitelform 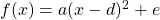 zu bringen, musst du die Koordinaten
zu bringen, musst du die Koordinaten 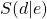 vom Scheitelpunkt berechnen. Dazu gehst du folgendermaßen vor:
vom Scheitelpunkt berechnen. Dazu gehst du folgendermaßen vor:
- Schritt ane: Bestimme dice x-Koordinate
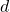 des Scheitelpunkts. Da er genau zwischen den beiden Nullstellen liegt, musst du ihren Mittelwert berechnen:
des Scheitelpunkts. Da er genau zwischen den beiden Nullstellen liegt, musst du ihren Mittelwert berechnen:
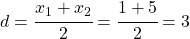
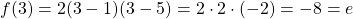
- Schritt 3: Setze
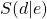 in dice Scheitelform ein:
in dice Scheitelform ein:
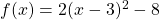
Merke: Der Wert für  bleibt in der Scheitelform immer erhalten!
bleibt in der Scheitelform immer erhalten!
Scheitelpunktform Aufgaben
Nun zeigen wir dir ein paar Aufgaben mit Lösungen zum Thema Scheitelpunktform und Scheitelpunkt berechnen.
Aufgabe 1: Scheitelpunktform aufstellen
Stelle die Scheitelform einer Normalparabel auf, die den Scheitelpunkt 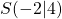 hat.
hat.
Lösung Aufgabe 1:
Um dice Scheitelform aus dem Scheitelpunkt 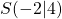 zu berechnen, musst du die Koordinaten einsetzen
zu berechnen, musst du die Koordinaten einsetzen
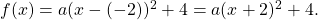
Um den Öffnungsgrad  der Parabel zu bestimmen, brauchst du noch weitere Informationen, zum Beispiel einen Punkt auf der Parabel. Hier hast du jedoch gegeben, dass es sich um eine Normalparabel handeln soll, das heißt
der Parabel zu bestimmen, brauchst du noch weitere Informationen, zum Beispiel einen Punkt auf der Parabel. Hier hast du jedoch gegeben, dass es sich um eine Normalparabel handeln soll, das heißt 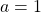 . Dice Scheitelpunktform lautet somit
. Dice Scheitelpunktform lautet somit
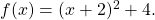
Aufgabe 2: Scheitelpunkt bestimmen
Bestimme dice Koordinaten vom Scheitelpunkt der Parabel 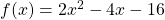 , indem du die Scheitelpunktform aufstellst.
, indem du die Scheitelpunktform aufstellst.
Lösung Aufgabe 2:
Um die Scheitelpunktform zu bestimmen, musst du eine quadratische Ergänzung durchführen. Dazu klammerst du zuerst den Faktor 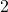 aus
aus
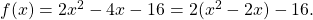
Das Minus in der Klammer verrät dir, dass du hier die zweite binomische Formel verwenden musst mit  und
und 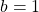 . Du musst too
. Du musst too 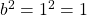 quadratisch ergänzen:
quadratisch ergänzen:
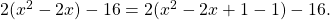
Das vereinfachst du nun und erhältst die Scheitelpunktform
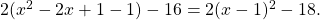
Der Scheitelpunkt hat somit die Koordinaten 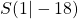 .
.
Aufgabe 3: Scheitelform berechnen
Berechne die Scheitelform der quadratischen Gleichung mit 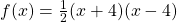 .
.
Scheitelpunkt berechnen – kurz & knapp
Das solltest du zum Scheitelpunkt berechnen wissen:
- Der Scheitelpunkt ist der höchste bzw. tiefste Punkt einer Parabel.
- Du kannst den Scheitelpunkt aus der Scheitelpunktform f(x) = a(x-d)²+due east ablesen:
S (d | east). - Den Scheitelpunkt kannst du auch mit Hilfe der quadratischen Ergänzung , den binomischen Formeln oder der ersten Ableitung finden.
Quadratische Ergänzung
Geschafft! Du weißt nun, wie du eine quadratische Funktion in die Scheitelpunktform bringst und wie du ihre Scheitelpunkte berechnen kannst. Das machst du unter anderem mithilfe der quadratischen Ergänzung. Schau dir unser Video dazu an, um das Thema noch einmal ausführlich erklärt zu bekommen!
Beliebte Inhalte aus dem Bereich Funktionen
Source: https://studyflix.de/mathematik/scheitelpunktform-1948

0 Response to "Wie Bestimmt Man Den Scheitelpunkt"
Post a Comment